使用正则表达式匹配 3 的倍数
Jul 4, 2018
北邮的考试周,与别处是不同的。都是近两周的时间,经常穿插着空挡,预备着可以随时抱佛脚。复习的人,傍午傍晚复习崩溃,每每花四十分钟,拿出手机 —— 这是十年前的事情,现在根本没有这么多时间。 —— 在教室做着,热热的玩了休息;倘肯多花一小时,便可以水一水群,或者看一看知乎,做精神娱乐了,如果歇到八九个小时,那就能回一趟宿舍,但这些学生,多是害怕考试挂科的,大抵没有这样阔绰。只有做学霸的,才踱进教室西边的宿舍里,拿起电脑,慢慢地玩游戏。
我从十七岁起,便在校内的计院当学渣。在考试周周末下午歇息时,看到了一个有趣的网站。便顶着要挂科的压力,好好地把玩了一番这个网站。网站的问题大抵是很常规的正则表达式的问题,但其中的 Triples 很有意思,题意大概如下:
使用正则表达式匹配出全部 3 的倍数。
3 的倍数的各位相加的和也是 3 的倍数。这个特征相信各位小学就会。根据这句话,我们就可以构造出一个判断 3 的倍数的有限状态自动机。因为 3 的余数只可能为 0,1,2,我们需要 3 个状态即可。三个状态的含义如下:
-
状态 A:当前各位数字相加为 3 的倍数
-
状态 B:当前各位数字相加的结果模 3 等于 1
-
状态 C: 当前各位数字相加的结果模 3 等于 3
再加上每一位上的数字只可能为 0-9,我们很容易就可以画出如下的有限状态自动机:
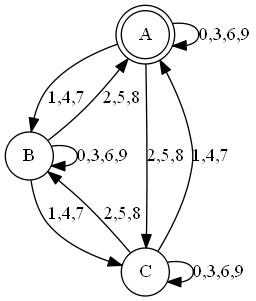
画出了自动机就是成功的一半,我们现在需要的就是把这个自动机转化为正则表达式。步骤如下:
首先,就自动机列出方程,也就是写出我们怎么到达各个状态的:
A = A[0369] | B[258] | C[147] | ∅
B = A[147] | B[0369] | C[258]
C = A[258] | B[147] | C[0369]其中 ∅ 指初始状态。这个方程看起来有一点磨叽,因此我们使用 x 指代 {0,3,6,9},y 指代 {1,4,7},z 指代 {2,5,8}。现在这个方程可以写成这样:
A = Ax | Bz | Cy | ∅
B = Ay | Bx | Cz
C = Az | By | Cx我们的目标就是消去 B,C。由正则表达式的特性,我们知道: X = Xw | Y 有解 X = Yw*,
因此对于形如 X = Xw | Y | Z的公式,我们有解为 X = (Y | Z)w*。方程可以简化如下:
A = (Bz | Cy | ∅)x*
B = (Ay | Cz)x*
C = (Az | By)x*稍有常识的人都可以看出,C 很容易被消去。
A = (Bz | (Az | By)x* y | ∅)x*
B = (Ay | (Az | By)x* z )x*再消去 B,我们得到
A = x* (z x* y x*)* |
Ay x* (y x* z x*)* z x* (z x* y x*)* |
Az x* z x* (y x* z x*)* z x* (z x* y x*)* |
Ay x* (y x* z x*)* y x* y x* (z x* y x*)* |
Az x* z x* (y x* z x*)* y x* y x* (z x* y x*)*对于形如 X = u | Xv | Xw的方程,有解 X = u (v | w)*,因此该表达式可以化简为
A = (x* | z x* y | y ( x | y x* z )* z | z x* z ( x | y x* z )* z | y ( x | y x* z )* y x* y | z x* z ( x | y x* z )* y x* y)*现在我们就可以写出最终的正则表达式辣:
^([0369]|[258][0369]*[147]|[147]([0369]|[147][0369]*[258])*[258]|[258][0369]*[258]([0369]|[147][0369]*[258])*[258]|[147]([0369]|[147][0369]*[258])*[147][0369]*[147]|[258][0369]*[258]([0369]|[147][0369]*[258])*[147][0369]*[147])*$进行测试,结果如下:
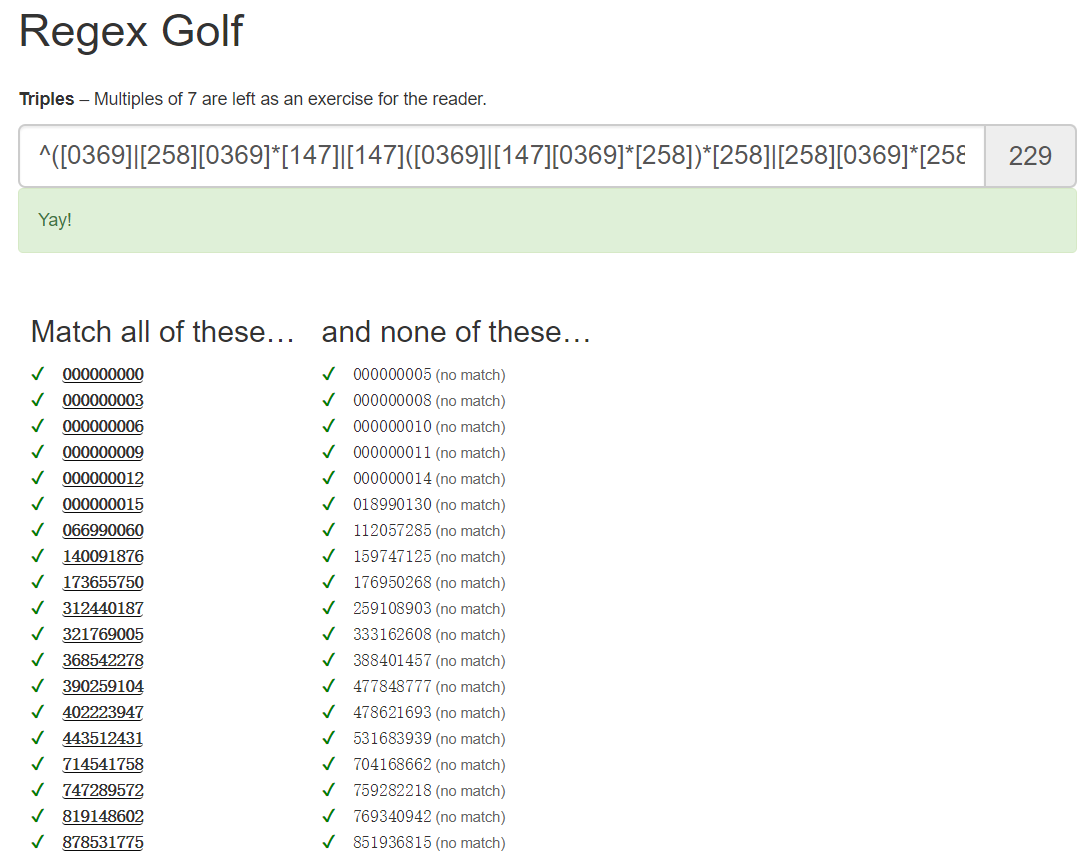
输入框的最后提示的式表达式的长度。就下面的排行榜来看,结果不算很好。
以上就是今天划水的全部内容。笔者继续休息去了(